UERJ, Sem Campus, Cálculo I, Provas - Profº Alexandre - P1 2014.2, Questão 3
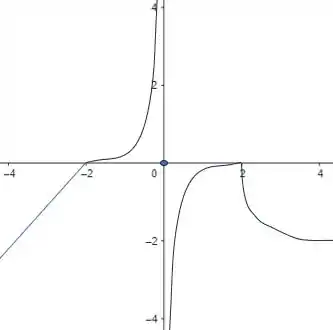
Esboce o gráfico de uma função com as seguintes características:
E se , então .
Passo 1
Eaee!!! Belezinha? Bom... queremos construir um gráfico com as seguintes características:
E se , então .
Muita informação né??
Mas vamos com calma, analisando informação por informação, que aos poucos vamos construindo 😉
Passo 2
Vamos primeiramente analisar essas duas informações:
Isso nos faz lembrar da função , que é dada da seguinte forma:
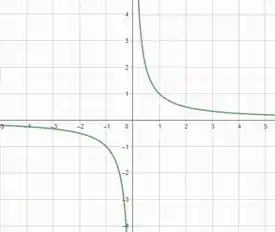
Dessa forma, invertendo a função, ou seja, fazendo , temos as nossas duas condições satisfeitas:
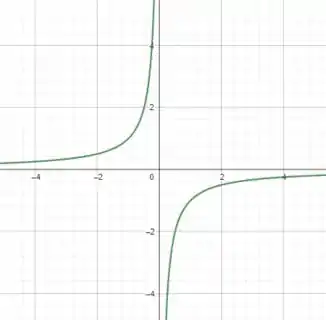
Passo 3
Agora, veja essa outra condição:
se , então .
Dessa forma, sabemos que pode ser ou . Portanto, temos:
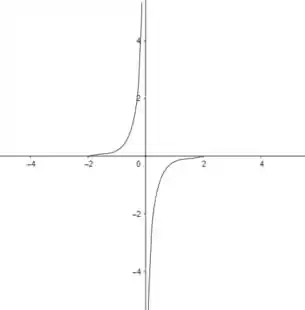
Passo 4
Agora, vamos adicionar essa outra condição:
Aqui vemos que tende a à medida que tende a . Logo, podemos definir que:
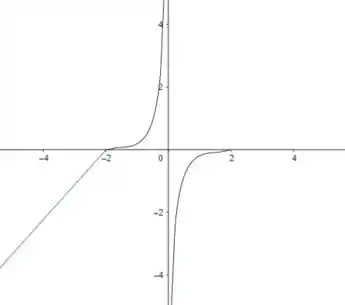
Passo 5
Agora, vamos aplicar nossa penúltima condição:
Aqui vemos que tende a à medida que tende a . Logo, podemos definir que:
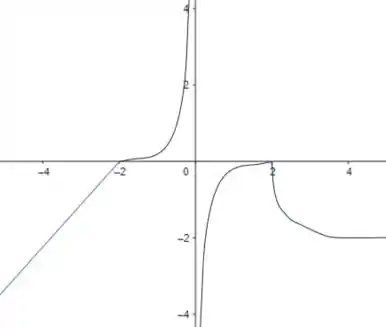
Por fim, aplicando a nossa última condição, se fizermos para , teremos que nosso domínio serão todos os números reais. Assim, temos:
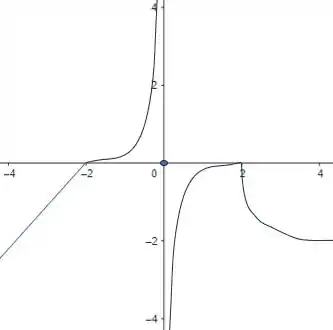
Entendeu direitinho? Responde aee ;)
Resposta
