Curvas Parametrizadas
Esboce a imagem de .
Passo 1
Mais direta que isso a questão não poderia ser... essa não dá nem pra enrolar rs
Então partiu analisar o que temos! Veja só, a coordenada vale e a vale . Daí tiramos que está entre e , enquanto está entre 2 e , show? Basta colocar os maiores e menores valor possíveis para as funções seno e cosseno!
E agora? Bom, já que tem esse cosseno ao quadrado, o mais instintivo é manipular essas trigonométricas e chegar em ! Como é seno, e , pois ,
Substituindo,
E aí está a equação cartesiana da nossa curva :D
Passo 2
Bom, agora que tiramos as trigonométricas ao quadrado da história, parece que ficou um pouco mais simples de esboçar, não? Veja só, chegamos numa parábola! Como é o que está ao quadrado, e seu coeficiente é negativo, então ela tem a boca virada para baixo! Como temos esse somado do lado direito da equação, então ela está deslocada em no sentido positivo de . Como o é e está entre e , nosso gráfico fica assim:
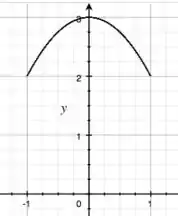
Viu o pico dela ali em ? E pronto, está aí :)
Resposta
