USP, São Carlos, Calculo 2, Listas de C2 - Grupo Coordenado 2022 - Lista 3 - Módulo 3, Questão 2a
Para cada item abaixo, encontre pelo menos duas funções a valores vetoriais e distintas satisfazendo a equação dada. (Conclui-se, assim, que uma parametrização de uma curva não é única.)
(a)
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado pediu pra gente encontrar duas parametrizações para a curva dada, usando o parâmetro .
Como está explicitamente em função de , podemos pensar em uma parametrização explícita para e assim teremos uma parametrização para . Além disso, se isolarmos na função dada, teremos uma função de e consequentemente uma nova parametrização.
Vamos lá!
Passo 2
Vamos dar uma olhadinha na nossa curva:
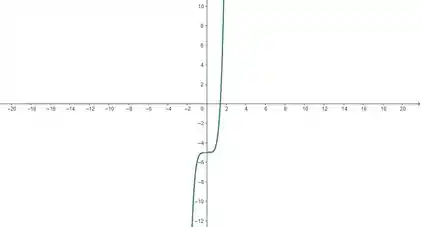
Ela pode ser representa tanto por quanto por . Usando a primeira equação, podemos chamar de e ganharemos uma parametrização para . Assim:
Então, uma parametrização é dada por:
Agora usando a equação na forma , podemos chamar de e teremos:
Portanto, outra parametrização para a curva seria dada por:
E temos nossas duas parametrizações.
Valeu, galera! Até a próxima! 😉