Ache a inclinação máxima da curva no intervalo .
Passo 1
Achar a inclinação máxima significa encontrar a maior derivada, pois é ela que dá a inclinação da curva. Então, primeiro vamos derivar a função da curva.
Observe que muda de sinal em e pois nesses pontos ela é nula. O sinal da derivada está representado no esquema abaixo.
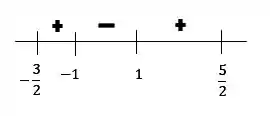
Passo 2
Sabendo que do ponto para o ponto a derivada está diminuindo, visto que em ela é nula, e que de para a derivada está aumentando, o maior valor da derivada só pode ser em uma das extremidades do intervalo (em ou em ). Então vamos substituir esses dois valores na derivada e ver qual é o maior.
Como a inclinação máxima da curva é .
Resposta
Exercícios de Livros Relacionados
Quantas retas tangentes à curva y = x / ( x + 1 ) passam pelo ponto ( 1 ,2 ) ? Em quais pontos essas retas tangentes tocam a curva?
Se G x = 4 x 2 - x 3 , encontre G ' ( a ) e use-o para encontrar equações das retas tangentes à curva y = 4 x 2 - x 3 nos pontos ( 2 ,8 ) e ( 3,9 ) .Ilustre a parte (a) traçando a curva e as retas tan
Encontre uma equação da reta tangente à curva y = 2 1 + e - x no ponto 0,1 .Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Encontre a equação da reta tangente à curva no ponto dado y = x - 1 x - 2,( 3,2 )
Esboce o gráfico de uma função f para a qual f 0 = 0 ,f ' 0 = 3,f ' 1 = 0ef ' 2 = - 1