UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profs, Emerson e Raimundo - Lista 5, Questão 5a
Um avião de caça dá um vôo rasante, percorrendo a trajetória determinada pelo gráfico da função e efetua seus disparos segundo a direção de uma reta tangente como mostra a figura
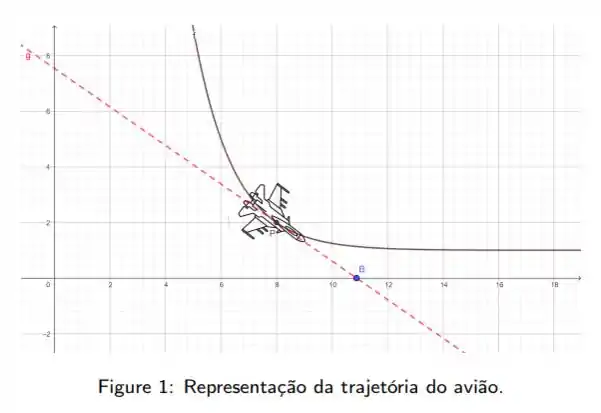
Determine a equação da reta tangente ao gráfico de em um ponto genérico .
Passo 1
Oiie, tudo bem?
O avião descrito no enunciado descrever uma trajetória que segue o gráfico da função
e faz um disparo que segue a tangente a esta curva, como indicado na figura
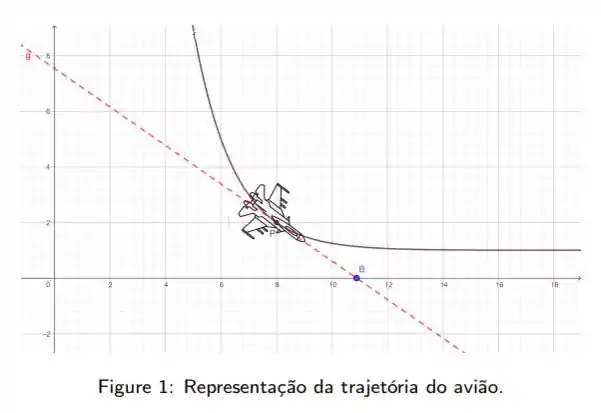
nesta primeira alternativa precisamos
Determine a equação da reta tangente ao gráfico de em um ponto genérico .
para isso precisamos lembrar que a inclinação da reta tangente é dada pela definição de derivada como
Vamos então usar o ponto arbitrário e avaliar esse limite! Saca só!
Passo 2
Aplicando a função e o ponto em nossa definição, temos que
podemos evidenciar o termo de forma que
ou, da mesma forma
Isso lembra uma dica que o professor deu nesta mesma lista mas em outra questão! Vem comigo!
Passo 3
Se fizermos a mudança , temos que
na questão desta mesma lista, o professor indica que
identificando que e , temos que
que é a inclinação de nossa reta, note que a reta em si obedecerá uma relação da forma
como a reta passa pelo ponto obtemos
de forma que
e, a equação da reta é simplesmente
Essa alternativa foi isso! Te vejo na próxima! Tchau Tchau!