UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profs, Emerson e Raimundo - Lista 5, Questão 5b
Um avião de caça dá um vôo rasante, percorrendo a trajetória determinada pelo gráfico da função e efetua seus disparos segundo a direção de uma reta tangente como mostra a figura
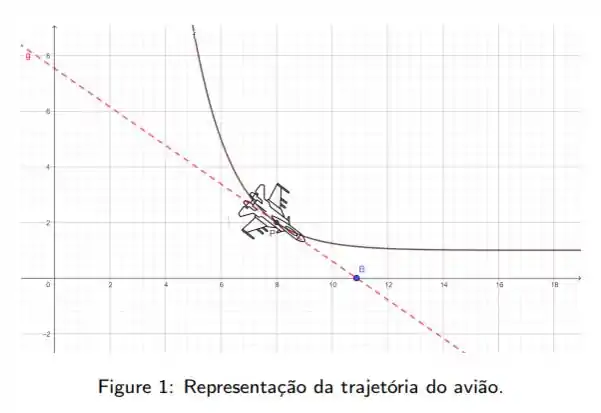
Se o avião dispara a partir do ponto , em que coordenada atingirá o eixo das abscissas?
Passo 1
Oiie, tudo bem?
O avião descrito no enunciado descrever uma trajetória que segue o gráfico da função
e faz um disparo que segue a tangente a esta curva, como indicado na figura
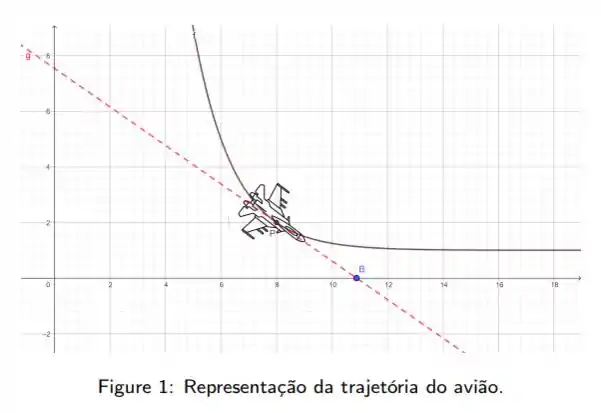
nesta primeira alternativa precisamos
Se o avião dispara a partir do ponto , em que coordenada atingirá o eixo das abscissas?
na alternativa anterior, para um ponto arbitrário , obtivemos a reta tangente
Vamos então usar o ponto e avaliar onde ela cruza o eixo das abscissas! Conhecido como eixo horizontal ahahahah! Vem comigo!
Passo 2
Usando o ponto dado, temos que reta se torna
quando temos que , temos que
e, portanto, o valor de é
a questão foi isso! Te vejo na próxima! Tchau Tchau!