UNICAMP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº Ricardo Martins - Lista sobre Derivadas, Questão 2.3
Calcule a reta tangente ao gráfico de no ponto . Faça um esboço.
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para descobrir a reta tangente à função no ponto .
Para isso, precisamos encontrar a derivada da função e usar essa informação para determinar a equação da reta que queremos. Essa equação é dada por:
Onde é o coeficiente angular da reta.
Lembrando que a função pode ser reescrita da seguinte forma:
E aí? Bora lá??!!
😉
Passo 2
Assim, aplicando a regra da potência para a função , temos:
Agora, podemos substituir o valor na derivada para encontrar o coeficiente angular da reta tangente:
Agora, precisamos determinar o valor de quando para encontrar o coeficiente linear.
Substituindo na função original, temos:
Então, o ponto pertence à reta tangente.
Passo 3
Agora, podemos escrever a equação da reta tangente usando o coeficiente angular e o ponto :
Simplificando a equação, temos:
Reorganizando os termos, obtemos:
Portanto, a reta tangente ao gráfico de no ponto é dada por .
Passo 4
Para esboçar esse gráfico, vemos que trata-se de uma reta positiva que “corta” o eixo em , ou seja:
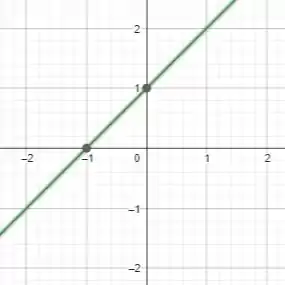
Entendeu direitinho? Responde aee ;)
Resposta
