UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 7
Considere a parametrização dada por . Determine a equação da reta tangente à trajetória de no ponto . Esboce a curva e reta na mesma figura.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma curva parametrizada e quer que a gente encontre a reta tangente a essa curva no ponto . Em seguida, esboçar a curva e a reta no gráfico.
Para encontrar a reta tangente de uma curva parametrizada, vamos seguir um passo a passo bem simples:
1. Vamos encontrar o ponto correspondente a
2. Calcular
3. Determinar , substituindo o ponto.
4. Substituit tudo na equação da reta tangente:
Com , nesse caso.
Vamos lá!
Passo 2
Para e , vamos ter:
Calculando a derivada de , temos:
Aplicando o ponto na derivada:
Agora basta substituir os vetores que encontramos na equação da reta tangente:
Somando cada componente:
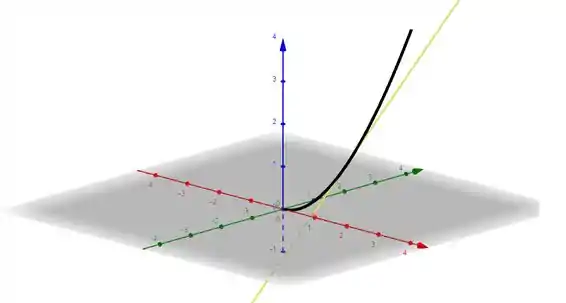
Agora a gente pode usar um software pra nos ajudar a plotar a plotar a curva parametrizada junto com sua reta tangente. Basta escrevermos os dois vetores, e , e teremos a curva parametrizada (em preto) e a reta tangente no ponto , em amarelo:
Prontinho, galera! Até a próxima! 😉