USP, Sem Campus, Cálculo 1, Listas de Cálculo 1 - USP - Lista 1, Questão 3.17
Considere todas as retas que são simultaneamente tangentes às parábolas e . Então o produto dos coeficientes angulares dessas retas é:
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinarmos o produto dos coeficientes angulares de todas as tangentes das parábolas e .
Para ficar melhor nossa visualização, vamos plotar as parábolas:
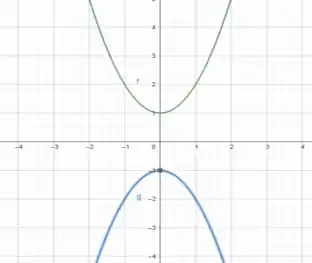
Bom, nós sabemos que a derivada de uma função nos dá o coeficiente angular da reta tangente à função em qualquer ponto do gráfico. Então, nós vamos conseguir encontrar o produto dos coeficientes angulares derivando as funções que descrevem essas parábolas. Assim, vamos encontrar um valor que relaciona o produto desses coeficientes.
Agora vamos lá!! 😉
Passo 2
Bom... a questão nos fala em reta tangente, então vamos fazer as derivadas das duas funções:
E
Fazendo , onde é o multiplicador que queremos encontrar, temos:
Pelo gráfico do Passo 1, também já poderíamos concluir que por conta de as parábolas serem “espelhadas”.
Entendeu direitinho? Responde aee ;)
Resposta
b)