UFES– Cálculo 2 – P3 – Questão 3
Dada a curva , ache sobre esta curva um ponto cuja reta tangente passa pelo ponto
Passo 1
Oi, tudo bem? Essa questão parece complicada, mas vou ajudar e resolver passo a passo com você!
O problema nos dá uma curva vetorial
E pergunta qual é o ponto sobre essa curva cuja reta tangente passa pelo ponto
Vamos recordar como encontrar uma reta tangente?
Mas sabemos que essa reta tangente passa pelo ponto . Então sabemos que isso daqui é válido para um certo valor de
Só nos resta saber quem é esse e com ele em mãos, substituir novamente em e achar que ponto ele
Mas calma, vou fazer passo a passo com você!
Passo 2
Vamos começar achando a derivada dessa curva! A curva é:
E vamos derivar em relação a t:
Beleza?
E agora vamos supor um parâmetro que satisfaça aquela condição do passo 1:
Então temos o seguinte:
Como temos uma equação vetorial, podemos dividir em três equações distintas:
Temos três equações e duas incógnitas, então esse sistema é possível! Nossa missão agora é encontrar quem é esse
Passo 3
Resgatando nosso sistema:
Da primeira equação temos:
E substituindo na segunda:
Fazendo a distributiva nos parênteses e multiplicando tudo por dois temos o seguinte:
Nossa boa e velha Bhaskara!
Passo 4
Aplicando a fórmula de Bhaskara para achar as raízes:
Certinho? E agora, o que fazer com esse valor?
Substituir na curva! Isso porque determinamos qual é o parâmetro que faz com que a reta tangente da curva passe no ponto dado! E esse parâmetro nos diz em que ponto da curva isso acontece!
Nossa curva é:
Agora aplicando em temos:
Para :
Ou também para :
Qualquer um dos dois pontos é a resposta correta! Mas se você olhar com carinho as alternativas, verá que temos essas opções como resposta:
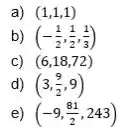assim a alternativa correta é a (C)
e é isso! Espero ter ajudado!