(a) Determine a equação da reta tangente ao gráfico no ponto
(b) Encontre a área da região do plano delimitada pela reta do item anterior, o gráfico de e o eixo
Passo 1
(a)Escolher e montar a equação da reta
Show de bola, vamos lá! Existem duas equações de reta possíveis:
As duas são válidas, mas as vezes só uma ajuda no que o enunciado pede. Como o enunciado pede a reta em um ponto de tangência e não a reta que passa por um ponto qualquer, a melhor equação é a segunda, onde .
Beleza, mas quem é esse ai mesmo? Essa constante vai ser a inclinação da reta tangente, que vai ser igual à:
Nossa equação de reta vai ser então:
E como o ponto de tangência é dado, temos:
Passo 2
Achar a inclinação da reta tangente
Agora vem a parte mais braçal: a inclinação da reta tangente. Pra isso, precisamos derivar primeiro. Então vamos lá:
Agora, no ponto de tangência, vamos ter:
Passo 3
Terminar de montar da equação da reta e ver o gráfico
Perfeito! Fechamos! Temos tudo pra montar a equação da reta. A reta vai ficar:
Graficamente:
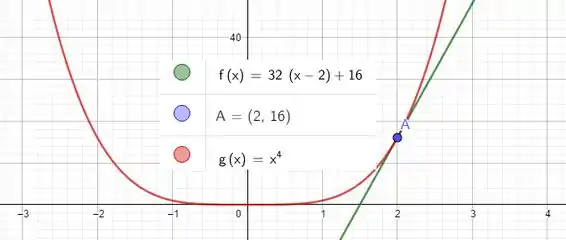
Passo 4
(b) Encontrar a região do enunciado
Infelizmente não acabamos ainda. A questão ainda pede uma área de uma região. Estando essa região delimitada por , o eixo e , graficamente teremos:
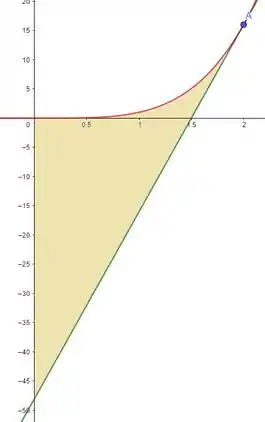
Portanto podemos entender essa área como a soma dessas áreas:
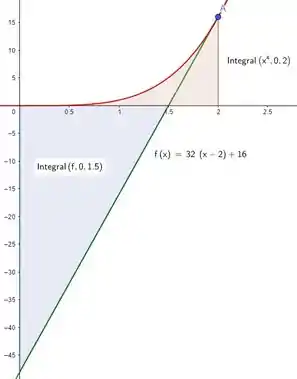
Menos essa última área:
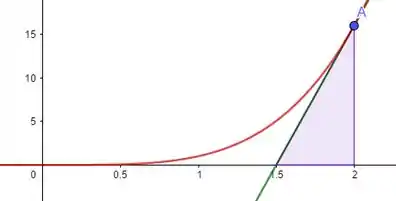
A primeira coisa que temos que fazer é encontrar a raiz da reta, beleza? Isso vai nos dar os limites de integração. Então partiu:
Como a área azul é negativa se calculamos por integrais, vamos calcular então usando um módulo:
Beleza, mas faltam duas áreas. A marrom vai ficar:
E pra fechar com chave de ouro, a área roxa:
Agora é só juntar os resultados: