UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profs, Emerson e Raimundo - Lista 5, Questão 4b
Encontre as equações das retas tangentes às curvas dadas nos pontos dados. Esboce o gráfico e a reta tangente.
Passo 1
Eaew, tudo certinho?
O enunciado nos dá a seguinte função e pontos
precisamos usar isso para calcular a reta tangente da função em ambos os pontos. Para isso precisamos lembrar que a derivada de uma função avaliada em um ponto é a inclinação da reta tangente neste ponto! Ou seja
Note que e . Sendo assim, vamos calcular a derivada e usar isso para esboçar a nossa reta! Vamos lá!
Passo 2
Aplicando a função e o ponto em nossa definição, temos que
Vamos multiplicar denominador e numerador por para obter
de forma que a inclinação é
ou seja, no ponto temos uma reta de inclinação . Ou seja
como temos que o ponto pertence a reta, precisamos que
e, a reta é a seguinte
o esboço do gráfico é
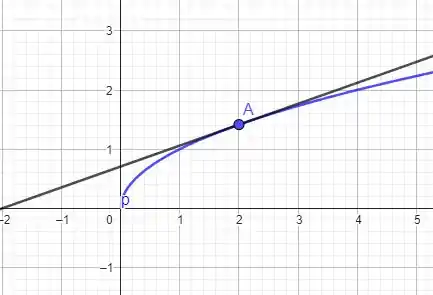
A questão foi isso! Te vejo na próxima! Tchau Tchau!