UFPA, Sem Campus, Cálculo I, Listas de Cálculo 1 - Profs, Emerson e Raimundo - Lista 5, Questão 4c
Encontre as equações das retas tangentes às curvas dadas nos pontos dados. Esboce o gráfico e a reta tangente.
e
Passo 1
Eaew, tudo certinho?
O enunciado nos dá a seguinte função e pontos
e
precisamos usar isso para calcular a reta tangente da função em ambos os pontos. Para isso precisamos lembrar que a derivada de uma função avaliada em um ponto é a inclinação da reta tangente neste ponto! Ou seja
Note que e . Sendo assim, vamos calcular a derivada e usar isso para obter as nossas retas! Note que também iremos precisar algumas propriedades da função módulo! Saca só!
Passo 2
Aplicando a função e o ponto em nossa definição, temos que
note que nas proximidades de , temos que , sendo assim, podemos simplificar a expressão para
ou simplesmente
ou seja, no ponto temos uma reta de inclinação . Ou seja
como temos que o ponto pertence a reta, precisamos que
e, a reta é a seguinte
Vamos calcular no outro ponto agora!
Passo 3
No outro ponto temos que
só que agora, nas proximidades de , temos que a função módulo é tal que , e portanto, novamente, podemos simplificar a expressão
de forma que
e, analogamente ao que fizemos anteriormente, a reta tangente é
O esboço do gráfico e de ambas as retas é
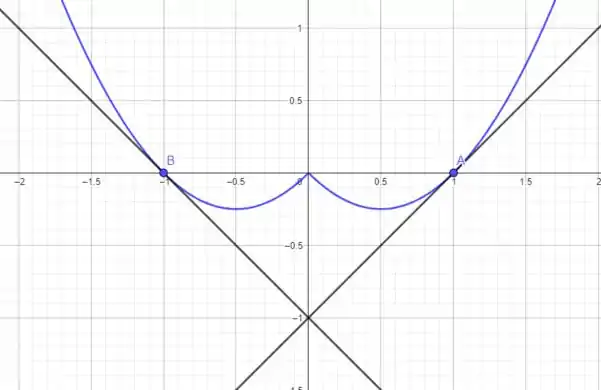
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
e