Encontre uma parábola que passa pelo ponto e cujas retas tangentes em e tenham inclinações e respectivamente.
Passo 1
Definindo a,b
Fala galera bonita, tudo certo? Bom, pra começar, a gente pode enunciar aqui a equação de uma reta tangente. Pra qualquer função , a reta tangente a ela no ponto terá sempre a seguinte cara:
Onde é a inclinação da reta, e é representada matematicamente pelo valor da primeira derivada no ponto de tangência, ou seja:
Como sabemos a cara da função, derivamos:
Até aqui tudo bem, mas pensa comigo: são três incógnitas pra achar e somente dois pontos pra trabalhar, tem algo errado aí! Bem, realmente tem, mas veja que na equação de , só duas incógnitas aparecem! E do enunciado, temos:
Opa! Conseguimos montar um sisteminha com esses valores! Saca só:
Multiplicando a primeira equação por 3, temos:
Somando as duas, chegamos a:
Usando esse valor na segunda equação, temos:
O que resulta em:
E bem, modelamos parte da parábola já:
Passo 2
Definindo c
Agora a gente vai achar o último parâmetro da parábola usando a única informação que não usamos ainda: o ponto , que pelo enunciado, faz parte dela. Sendo assim, temos:
E ta na mão! A equação vai ser:
Passo 3
Confirmação gráfica
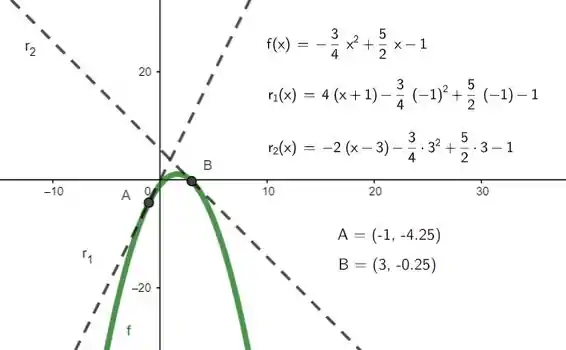
Essa parte aqui não precisa, mas é só pra ilustrar e ficar bonitinho pra vocês! Sendo:
As duas tangentes serão:
E o gráfico de considerando essas tangentes tem essa cara: