UFJF – Cálculo 1 – AV2 – 2019/2
3. Na figura a seguir, estão representadas uma função e a reta tangente ao gráfico dessa função no ponto .
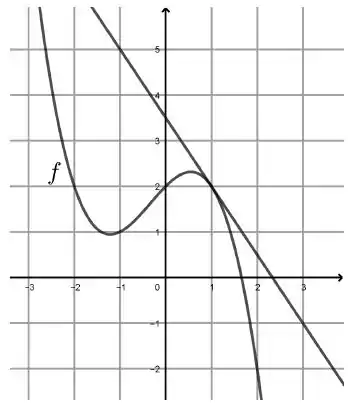
O valor da derivada é:
a)
b)
c)
d)
e)
Passo 1
Falaaa... nessa questão foi dado o gráfico de uma função e queremos achar a derivada no ponto
Pra isso vamos lembrar que a derivada de uma função no ponto é a inclinação da reta tangente.
No gráfico já foi dada essa reta tangente desenhada bonitinha.
Passo 2
Pra achar a inclinação da reta tangente vamos usar pontos que passem peles retas horizontais e verticais (a grade de fundo) que se cruzam, tipo o ponto e
Achando a inclinação da reta:
Então a derivada no ponto será:
Letra b
Resposta
Letra b
Exercícios de Livros Relacionados
Quantas retas tangentes à curva y = x / ( x + 1 ) passam pelo ponto ( 1 ,2 ) ? Em quais pontos essas retas tangentes tocam a curva?
Se G x = 4 x 2 - x 3 , encontre G ' ( a ) e use-o para encontrar equações das retas tangentes à curva y = 4 x 2 - x 3 nos pontos ( 2 ,8 ) e ( 3,9 ) .Ilustre a parte (a) traçando a curva e as retas tan
Encontre uma equação da reta tangente à curva y = 2 1 + e - x no ponto 0,1 .Ilustre a parte (a) fazendo o gráfico da curva e da tangente na mesma tela.
Encontre a equação da reta tangente à curva no ponto dado y = x - 1 x - 2,( 3,2 )
Esboce o gráfico de uma função f para a qual f 0 = 0 ,f ' 0 = 3,f ' 1 = 0ef ' 2 = - 1