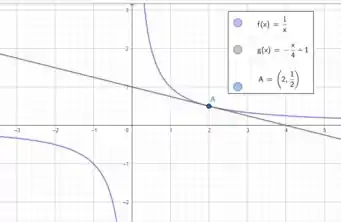
Parte 1: Determine a equação da reta tangente ao gráfico de no ponto de abscissa
Parte 2: Esboce o gráfico de e da reta tangente
Passo 1
Oi pessoal, tudo bem por aí? Essa é uma continuação! Agora nessa segunda parte vamos esboçar os gráficos!
Temos que nossa função é a hipérbole
E a derivada no ponto é
Encontramos também a equação da reta tangente nesse ponto
Agora nossa missão é colocar em um gráfico essas duas funções: e !

Bora lá!
Passo 2
As duas funções
Podem ser escritas no mesmo gráfico:
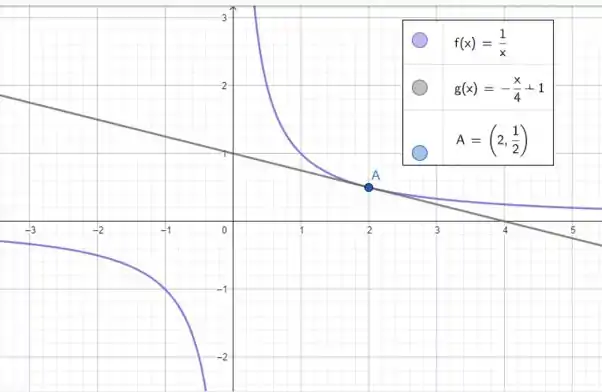
lembrando que o ponto de tangência vale tanto pra reta tangente quanto pra função! E está representado no ponto

E é isso! Até a próxima!
Resposta