Seja . Considere a função tal que
Sabendo que é um ponto de inflexão do gráfico de , faça o que se pede:
a) Determine e o valor da constante .
b) Determine .
c) Determine a equação da reta tangente ao gráfico de em
Passo 1
Usando a racionalização, podemos reescrever da seguinte maneira:
Cortando o do numerador com o denominador, temos:
Passo 2
Sabemos que a segunda derivada da função é a derivada de , certo?:
Então vamos derivar para encontrarmos :P
Então a nossa segunda derivada é
Passo 3
Para encontrarmos o valor da constante , vamos usar a informação de que o ponto de inflexão da função é . Bom, sabemos que o ponto de inflexão é o ponto onde a segunda derivada muda de sinal, seja de pra ou de pra .
O que importa, é que nesse ponto de inflexão, a segunda derivada vale , ou seja, :
Logo, substituindo o valor de em :
Passo 4
b) Você lembra que a integral de uma função é aquela função antes de derivarmos?
![]() Derivar Derivar
Derivar Derivar
Integrar Integrar
Antes de ter sido derivado, ele era o . Então o que vamos fazer para encontrarmos ???
Isso mesmo!! Integrar a sua derivada hahahaha
Do item anterior, temos que
Podemos separar em 3 integrais:
Resolvendo as integrais, temos:
Onde é a soma das constantes das 3 integrais.
Passo 5
Como é ponto de inflexão da função, ele está no nosso gráfico, então podemos substituir em para encontrarmos
Então
Passo 6
c) A equação de uma reta tangente a um gráfico tem esse formato olha:
Onde é a abscissa do ponto de tangência que queremos.
Nosso ponto de tangência , a pedido do enunciado, é .
Tendo que , sabemos que nosso coeficiente angular da reta, ou seja, a derivada no ponto de tangência , vai ser
O que faz sentido, pois o ponto é ponto de inflexão e a derivada nesses pontos vale 0.
Passo 7
Então vamos construir nossa reta tangente:
Logo, nossa reta tangente tem a equação
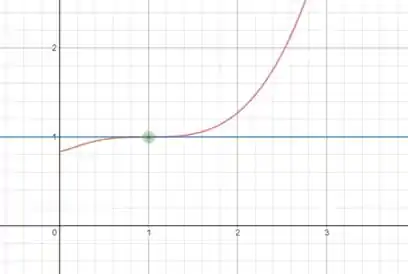
Abaixo temos em vermelho o gráfico de , em azul a reta tangente e em verde o ponto
Resposta
a)
b)
c)