UFRJ, Sem Campus, Cálculo 1, Listas de C1 - Profº Jair - Primeira Edição V1.3, Questão 4.3.1b
Seja uma função definida em , contínua em todo o seu domínio e satisfazendo as condições abaixo:
e
Suponha que o gráfico de é dado pela figura abaixo:
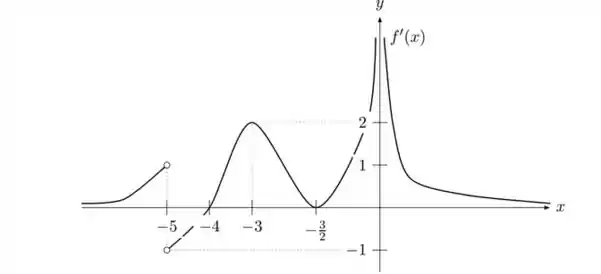
Responda, justificando, o que se pede:
Os pontos onde a reta tangente ao gráfico de é horizontal;
Passo 1
E aí gente, tudo beleza?
Nessa questão temos uma função , com a informação de algum dos seus pontos:
Também foi dado o gráfico da derivada de , ou seja,
Além disso, o enunciado também nos falou que:
Nesse item precisamos determinar os pontos onde a reta tangente ao gráfico da função é horizontal.
Mas, a reta tangente ao gráfico de uma função é justamente a derivada, . Se ela for horizontal, a sua inclinação é nula, então vale:
Portanto, vamos procurar esses pontos!
Passo 2
Bom, vamos analisar o gráfico:
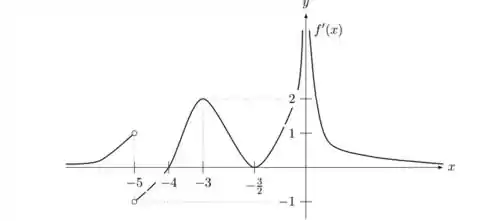
Em:
Temos . Portanto, nesses pontos a tangente à curva de é horizontal.
É issooo! Obrigado pessoal!
Até a próxima 😊