UNICAMP – Cálculo 1 – Lista 3 – Limite e Continuidade
1. Um tanque com capacidade para 1000 litros de água é drenado pela base em meia hora. Os valores na tabela mostram o volume de água remanescente no tanque (em litros) após minutos.
c) Use um gráfico da função para estimar a inclinação da tangente em . (Essa inclinação representa a razão na qual a água flui do tanque após 15 minutos.)
Passo 1
Falaaa... tudo bem??
Nessa questão vamos usar o gráfico da função. Esse gráfico conseguimos plotando esses ponto num gráfico.
Daí encontramos o ponto , que é em e .
Traçamos uma reta que seja tangente a esse ponto, ou seja, uma reta que só encoste nesse ponto, no gráfico.
Pra calcular a inclinação de uma reta qualquer usamos:
Passo 2
Usando gráfico:
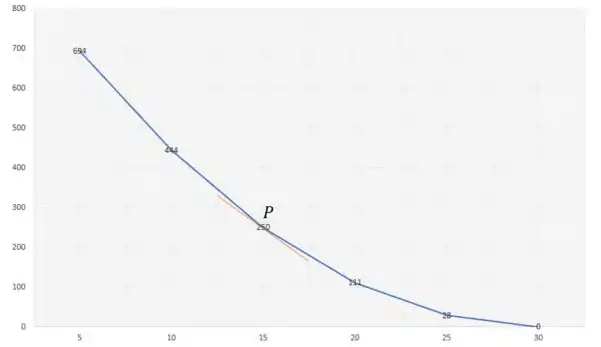
Repara na linha laranja que só encosta no ponto . Essa é a reta tangente em .
Agora queremos calcular a inclinação dessa reta laranja e usaremos:
Pra encontrar esses pontos vai ser no olhômetro mesmo... Até porque queremos calcular só uma estimativa.
Para temos (já que está entre e ) e para temos .
Para temos 325 e para temos 175.
Calculando: