UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista de Derivadas 2022.2, Questão 6d.
6 – Seja
d) Calcule , identifique o seu domínio e esboce seu gráfico.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nessa questão temos uma função definida por partes e nosso objetivo é calcular a derivada de , determinar o domínio de e esboçar seu gráfico.
Tem ideia de como fazemos isso? 🤔
Para calcular a derivada de uma função definida por partes, é necessário determinar a derivada em cada uma das partes separadamente e, em seguida, juntá-las.
Para esboçar o domínio da função definida por partes, é necessário determinar os pontos de descontinuidade, que ocorrem nos limites entre as partes da função. Em cada uma das partes, o domínio é o intervalo correspondente. Ou seja, são os possíveis valores para para a função ser definida.
Sacou? Bora começar! 😉
Passo 2
Calculando a derivada de pelo método de derivação polinomial, temos
Logo, a derivada de será
Tranquilo até aqui? 🤔
Passo 3
Para determinar o domínio de , vemos quais são os possíveis valores que pode admitir para a função ser determinada.
Como se trata de duas retas ( e ) pode assumir qualquer valor dos números reais, ou seja
E por fim, para esboçar o gráfico de , olhamos para as partes de . Quando , o gráfico de será da reta , mas se , o gráfico será da reta .
Juntando essas duas retas em seus devidos intervalos de , temos
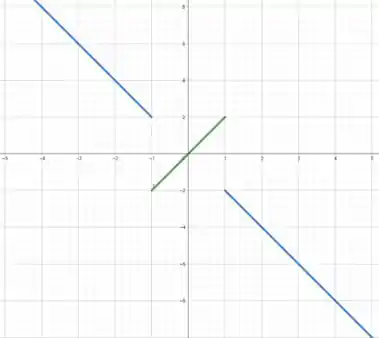
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍