UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Listas de Cálculo 1 - Profª Lilian Brambila - Lista 2 - Funções, Questão 4f
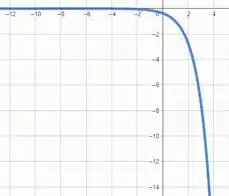
4. Com base no domínio, contra-domínio e imagem encontrado no exercício 1, faça o esboço das funções abaixo. Para a funções trigonométricas também exiba o período da função.
f)
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nessa questão queremos esboçar o gráfico da função dada com base no seu domínio, contradomínio e imagem. Além disso, queremos obter o período da função quando for possível.
Como fazemos isso? 🤔
Primeiro, vamos relembrar o que é domínio, contradomínio e imagem.
De forma resumida, O domínio de uma função é o conjunto de todos os valores possíveis de entrada, ou seja, é o conjunto de valores que pode assumir.
Já o contradomínio é o conjunto de todos os valores possíveis de saída, ou seja, é o conjunto de valores que pode assumir.
E por último, a imagem é o conjunto de todos os valores que a função realmente assume quando avaliada no seu domínio. Em outras palavras, é o conjunto de todos os valores de que são obtidos quando varia no domínio.
Lembra disso? 😁
Passo 2
Já o período de uma função é o menor número tal que para todo no domínio da função. Em outras palavras, a função tem um comportamento que se repete a cada unidades de .
Bacana, não é? 😎
A função que foi dada é
Perceba que a função é definida para qualquer valor de real, ou seja, para também não vai ser diferente
Já o conjunto imagem e o contradomínio são dados pelos possíveis valores que a função assume.
Sabemos que varia entre e , portanto, também vai variar no mesmo intervalo, só que negativo
Tranquilo até aqui? 🤔
Passo 3
Sabemos como é o gráfico da função ... quando é menor que , a função tende a e conforme aumenta, a função cresce muito rapidamente.
Então podemos imaginar que a função tem exatamente o mesmo comportamento, porém deslocada uma unidade para a direita e que por sua vez, a função será a função porém espelhada para o semieixo negativo de (lado de baixo do eixo )
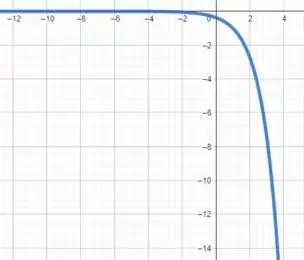
E como a imagem da função não se repete nenhuma vez, podemos dizer que a função não tem período.
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
