UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Listas de Cálculo 1 - Profª Lilian Brambila - Lista 2 - Funções, Questão 2a
Para cada função , faça o seguinte: encontre, se houver, a raíz; estudo o sinal da função; verifique se a função é crescente, decrescente ou constante; esboce o gráfico, apresentando todas as informações obtidas sobre tal função. Justifique todas as afirmações
a)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma função e nos pede algumas coisinhas:
- Encontrar o sinal da raiz (se houver), ou seja, encontrar o(s) ponto(s) que tocam o eixo ;
- Verificar se a função é crescente, decrescente ou constante. Podemos fazer isso analisando se a derivada é positiva ou negativa;
- Esboçar o gráfico da função, analisando as raízes e o crescimento/decrescimento/constância da função.
Não entendeu? Então bora junto 😉
Passo 2
Bom... dessa forma, primeiramente fazendo para encontrarmos se tem raiz:
Logo, vemos que a função tem uma raiz.
Passo 3
Agora, vamos fazer a derivada da função para verificar se ela é crescente, decrescente ou constante:
Dessa forma, como a derivada é negativa, então a função é decrescente.
Passo 4
Por fim, esboçando o gráfico, vemos:
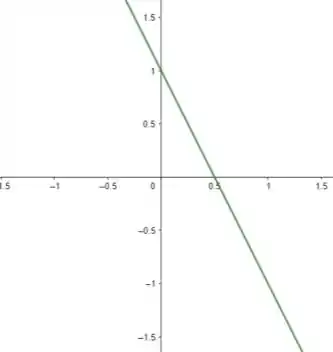
Entendeu direitinho? Responde aee ;)
Resposta
Raiz em
Decrescente
