UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 29ivh
Considere em cada um dos itens abaixo a função dada por e em seguida determine o que se pede:
h) Esboce o gráfico de .
Passo 1
Fala, galera! Vamos resolver essa questão.
O enunciado nos deu uma função , e pediu pra gente esboçar o gráfico dela.
Pra isso, vamos analisar nossa função, seus pontos críticos, de inflexão, assíntotas e onde ela intercepta os eixos do plano cartesiano.
Vamos lá!
Passo 2
Galera, nos itens anteriores nós verificamos, derivando a função e igualando a zero, que temos um único ponto de máximo em . Nós também vimos que a função muda de concavidade em .
A gente sabe que é um ponto crítico, porque a o denominador não pode zerar e o logaritimo de zero é indefinido. Mas quando , podemos ter uma assíntota, então vamos verificar calculando o limite:
E quando , vamos ter:
Podemos aplicar L’Hospital:
Então, temos uma assíntota em e em .
Pra saber onde a função intercepta o eixo , podemos fazer :
Isso acontece quando . Então, a função cruza o eixo em .
Com essas informações já podemos esboçar a função:
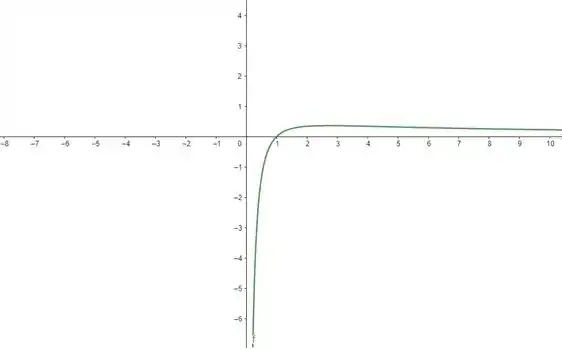
Prontinho, galera! Até a próxima! 😉