UFMG, Sem Campus, Equações Diferenciais B, P1 - 2022.2, Questão 1a
Considere a função definida no intervalo .
Esboce os gráficos das suas extensões par e ímpar, de período , no intervalo .
Passo 1
Oiie, tudo certinho?
Temos a função
definida no intervalo . Precisamos escrever a sua extensão par e a sua extensão ímpar! Mas como fazemos isso? A extensão par de uma função de período é tal que
e
em que nosso caso . Agora, a extensão ímpar será da forma
, e
Vamos aplicar para a nossa função!
Passo 2
Usando então que , temos que a expansão par é tal que
e
o esboço no intervalo terá o seguinte formato
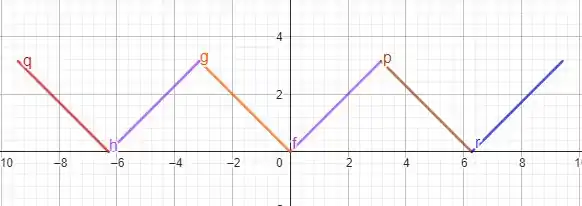
a extensão ímpar será agora
, e
o esboço do gráfico é tal que
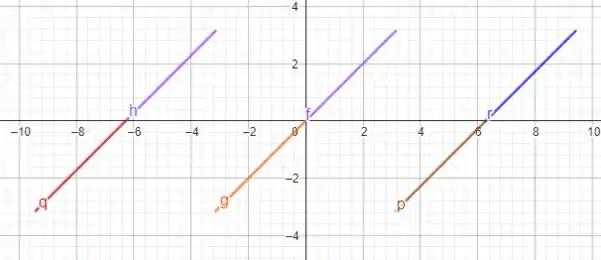
A primeira alternativa foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica