Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Esboço de Curvas

Ver Teoria
Exercício 104123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

UFF, Niterói - Praia Vermelha, Cálculo IA, P2 - 2022.2, Questão 1e

Considere a função f x = x e - x , definida em seu maior domínio possível.

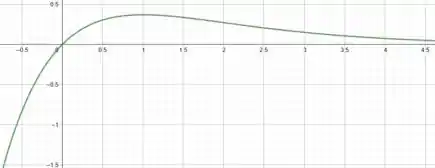
e) Faça um esboço do gráfico, utilizando todas as informações dos itens anteriores.

Passo 1

Eaí galera, tudo tranquilo?

Bom, nesse item precisamos unir todas as informações dos itens anteriores dessa questão para esboçar o nosso gráfico da função:

f x = x e - x

Tínhamos visto que:

1 )   f ( x ) tem assíntota horizontal em 0 quando x → + ∞ .

2 )   f x não têm assíntotas verticais.

3 )   f x   é   c r e s c e n t e   s e   x ∈ - ∞ ,   1 f x é   d e c r e s c e n t e   s e   x ∈ 1 , ∞ x = 1   é   p o n t o   d e   m á x i m o   l o c a l

4 )   x ∈ - ∞ , 2 ∴ f   t e m   c o n c a v i d a d e   p a r a   b a i x o x = 2 ∴ p o n t o   d e   i n f l e x ã o   d e   f x ∈ 2 , ∞ ∴ f   t e m   c o n c a v i d a d e   p a r a   c i m a

Prontinho! Com base nessas informações precisaremos esboçar o gráfico da função!

Passo 2

Da informação 1 ) , temos que:

1 )   f ( x ) tem assíntota horizontal em 0 quando x → + ∞

Ou seja, quando x tá tendendo a infinito, nossa curva tende a 0 . Com isso já podemos esboçar uma parte do gráfico:

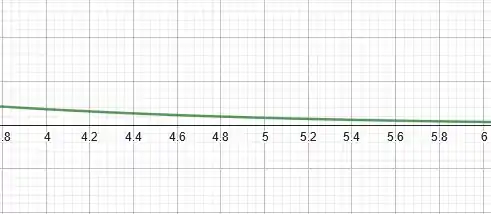
Beleza!

Vimos também que, quando x →   - ∞ nossa função não tem assíntota horizontal pois f ( x ) tende a - ∞ . Logo, na outra extremidade da função, devemos ter algo do tipo:

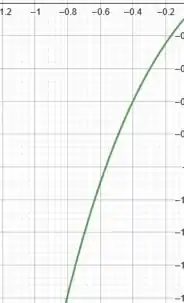
Ok! Vamos prosseguir!

Passo 3

Da informação 3 ) temos que:

f x   é   c r e s c e n t e   s e   x ∈ - ∞ ,   1 f x é   d e c r e s c e n t e   s e   x ∈ 1 , ∞ x = 1   é   p o n t o   d e   m á x i m o   l o c a l

E, da informação 4 ) também temos que:

x ∈ - ∞ , 2 ∴ f   t e m   c o n c a v i d a d e   p a r a   b a i x o x = 2 ∴ p o n t o   d e   i n f l e x ã o   d e   f x ∈ 2 , ∞ ∴ f   t e m   c o n c a v i d a d e   p a r a   c i m a

Juntando essas informações, temos:

x ∈ - ∞ ,   1 ∴ f   é   c r e s c e n t e   e   t e m   c o n c a v i d a d e   p a r a   b a i x o x = 1   é   p o n t o   d e   m á x i m o   l o c a l ,   c o n c a v i d a d e   p e r m a n e c e   p a r a   b a i x o . x ∈ 1,2 ∴ f   é   d e c r e s c e n t e   m a s   a   c o n c a v i d a d e   p e r m a n e c e   p a r a   b a i x o

Com essas informações, conseguimos desenhar:

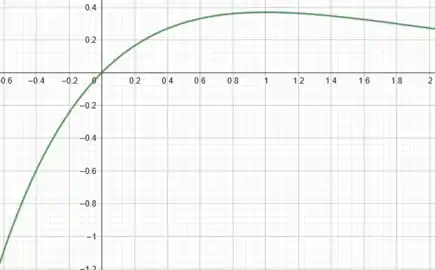
Vamos continuar analisando:

x ∈ 2 , ∞ ∴ f   é   d e c r e s c e n t e   e   p o s s u i   c o n c a v i d a d e   p a r a   c i m a .

Com essa última informação conseguimos unir todo o intervalo de f para desenhar sua curva.

Ficamos com o seguinte esboço:

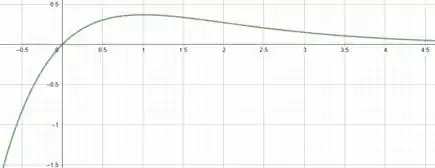
Aeee! Muito bom gente!

Finalizamos mais uma questãozinha.

Vocês curtiram? Responde Aí!

Resposta

Exercícios de Livros Relacionados

Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh ⁡ t y = cosh ⁡ t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen ⁡ θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen ⁡ θ
r = 9 6 + 2 cos ⁡ θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica