UFF, Sem Campus, Cálculo IA, AD1 - Pré-Cálculo - 2023.1 - Parte 2, Questão 4
Considere funções:
E
Encontre as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados.
Esboce o gráfico de . Explique a construção do gráfico da função , usando transformações em gráfico (translações, reflexões...) a partir do gráfico da função Descreva essas transformações em palavras.
Responda qual é o domínio da função .
Levando em consideração os gráficos obtidos nos itens anteriores e o gráfico da função , esboce o gráfico da função .
Responda qual é a imagem da função .
Observando o gráfico da função , dê os intervalos do domínio em que a função é decrescente. Esboce o gráfico da função e da função . Explique a construção desses gráficos.
A função é par? É ímpar? Nem uma coisa e nem outra? Explique!
A função é par? É ímpar? Nem uma coisa e nem outra? Explique!
Passo 1
Eaee!!! Belezinha? Bom... vemos que essa questão tem várias perguntinhas haha.
Mas vamos devagarinho buscar entender ela como um todo, certinho?
Passo 2
Bom...primeiro vamos encontrar as coordenadas dos pontos em que o gráfico da função corta os eixos coordenados.
Seja :
- Para :
- Para :
Logo, o cruzamento com os eixos se dá em: .
Passo 3
Agora, a questão nos pede para esboçar o gráfico de , explicar a construção do gráfico da função , usando transformações em gráfico (translações, reflexões...) a partir do gráfico da função e descrever essas transformações em palavras.
Bom, esboçando o gráfico, temos:
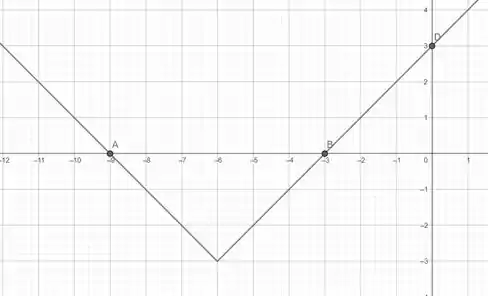
Vemos que pode ser construída a partir de usando as transformações:
- Translação em para esquerda em unidades;
- Translação em para baixo em 3 unidades.
Passo 4
Agora, queremos saber do domínio da função.
O domínio de :
- ;
Portanto, considerando os intervalos encontrados e verificando se as condições acima foram atendidas, temos que o domínio é dado pelo seguinte intervalo:
Passo 5
Agora, a questão nos pede para esboçar o gráfico da função , levando em consideração os gráficos obtidos nos itens anteriores e o gráfico da função .
Bom, esboçando o gráfico, temos:
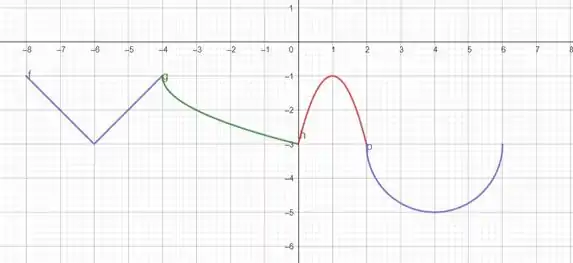
Passo 6
Agora, analisando o gráfico acima, podemos definir que a imagem está em .
Passo 7
Agora, a questão nos pede para dar os intervalos do domínio em que a função é decrescente. Também nos pede para esboçar o gráfico da função e da função e explicar a construção desses gráficos, observando o gráfico da função .
Bom... esboçando o gráfico, temos:
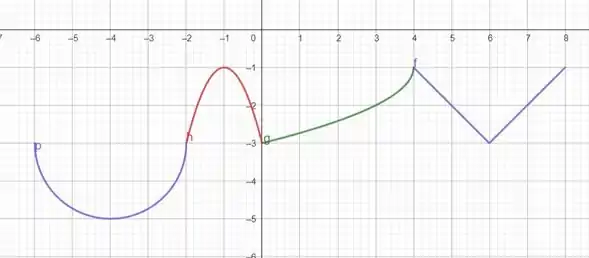
Vemos que a função é decrescente em .
Passo 8
Agora, devemos explicar o sentido de .
Bom... trata-se apenas da reflexão do eixo .
Passo 9
Agora, devemos explicar .
Aqui, o que estava do lado negativo de passou para o lado positivo de .
Portanto, nenhuma das funções é par ou ímpar, dado que não há simetria com nenhum eixo.
Entendeu direitinho? Responde aee ;)
Resposta
No texto