UFF, Sem Campus, Cálculo IA, AD1 - Pré-Cálculo - 2023.1 - Parte 2, Questão 1
Considere as funções e .
O gráfico da função é parte de uma curva conhecida. Esboce o seu gráfico e explique a construção desse gráfico identificando a curva que dá origem a ele. Justifique!
A partir do gráfico da função explique como é possível construir o gráfico da função usando três transformações em gráfico (translações, reflexões...). Descreva essas transformações em palavras. Esboce o gráfico da função .
Passo 1
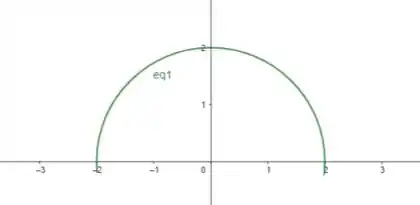
Eaee!!! Belezinha? Bom... seja . Podemos manipular da seguinte forma:
Portanto, é a parte positiva da circunferência de raio centrada em .
Passo 2
Bom... em seguida, seja . Manipulando, temos:
Passo 3
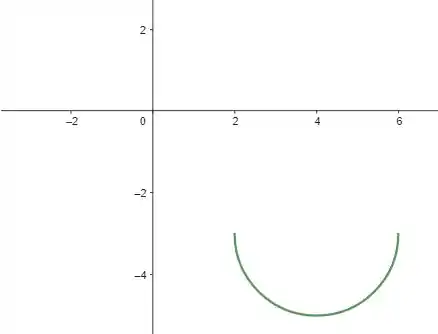
Agora, a partir do gráfico de , o gráfico de é construído de acordo com as seguintes transformações:
- Deslocamento em para a direita em unidades;
- Deslocamento em para baixo em unidades (translação);
- Reflexão devido ao sinal negativo antes da raiz.
Assim, temos o seguinte gráfico:
Entendeu direitinho? Responde aee ;)
Resposta
Ei, a resposta está no passo a passo :)