UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Lista 2 de Exercícios, Questão 2b
Considere os vetores , e . Determine e represente graficamente:
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá três vetores, onde:
Agora, temos que fazer e representar graficamente.
Para isso, primeiramente temos que descobrir quem é o vetor e, em seguida, aplicar o módulo.
Não entendeu? Então bora junto 😉
Passo 2
Bom... fazendo a soma de vetores, temos:
Agora, aplicando o módulo, temos:
Representando graficamente o vetor, encontramos:
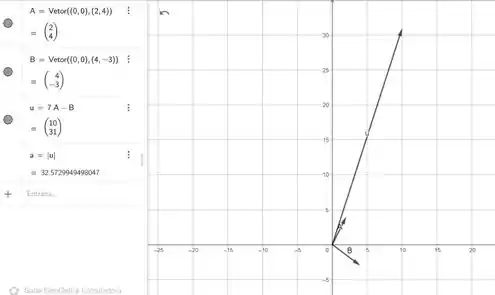
Onde .
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica