Dada a função . Determine:
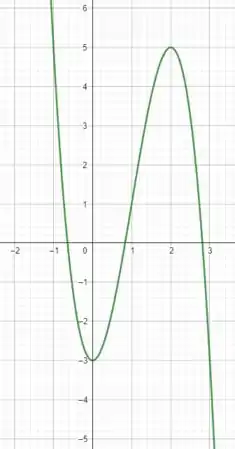
Faça um esboço do gráfico.
Passo 1
Eaew, tudo bem?
Vamos continuar essa questão! O enunciado nos dá a função
e, precisamos fazer o esboço do gráfico! Para isso vamos precisar de alguns resultados das alternativas anteriores! Nós obtemos os intervalos de crescimento como
e, decrescimento como
e
com um máximo local em e um mínimo local em . Essas informações já nos dão uma ideia de como será o gráfico! Vamos apenas analisar um pouco os limites no infinito da função! Saca só!
Passo 2
Temos que
Vamos colocar em evidência, temos que
pode ser dividido em dois limites
ou seja, temos que
Fazendo a mesma coisa para , podemos escrever que
Sendo assim, podemos esboçar o gráfico como
A questão foi isso! Te vejo na próxima! Tchau Tchau!
Resposta
Ao longo dos passos!