UTFPR, Sem Campus, Cálculo Diferencial e Integral 1, Listas de Cálculo 1 - Profª Lilian Brambila - Lista 2 - Funções, Questão 3c
Dadas as funções abaixo, verifique para cada uma delas:
- Se a concavidade da parábola é voltada para cima ou para baixo;
- Quais são, se houverem, as raízes da função;
- Encontre a interseção com o eixo vertical (eixo y);
- Encontre o vértice da parábola;
- Estude o sinal da função;
- Encontre os intervalos de crescimento e decrescimento da parábola, indicando qual é o ponto e o valor de máximo ou mínimo da função;
- Esboce o gráfico da função, exibindo o eixo de simetria da parábola e indicando a região na qual a função é positiva e na qual a função é negativa.
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá uma função quadrática , ou seja, já sabemos que tem uma parábola por aí né? Haha
Sabendo disso, a questão nos dá uma lista de tarefinhas que temos que realizar, então cada passo será sobre uma dessas tarefinhas, combinado?
Se desespere não que estamos juntos!!
😉
Passo 2
Bom... primeiramente queremos saber se a concavidade da parábola é voltada para cima ou para baixo.
Para isso, devemos analisar se termo que multiplica o é positivo ou negativo.
Vamos ver a função:
Como o termo que multiplica é positivo, então a parábola tem concavidade voltada para cima.
Passo 3
Agora, queremos descobrir as raízes da função.
Para isso, basta fazermos , se liga:
Que são as duas raízes das funções.
Passo 4
Agora, queremos encontrar a interseção com o eixo vertical, ou seja, quando :
Passo 5
Podemos encontrar o vértice da parábola descobrindo o ponto em que a derivada da função é zero.
Encontrando a derivada, temos:
Igualando a zero, temos:
E, substituindo o valor encontrado na função, temos o ponto do vértice:
Logo, o vértice está no ponto .
Passo 6
Agora vamos estudar o sinal da função, ou seja, quais valores reais de a função é positiva, negativa ou nula.
Como já descobrimos a concavidade da parábola e as suas raízes, temos então o seguinte estudo:
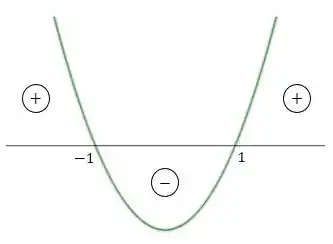
Analisando a figura acima, vemos os valores para os quais a função é positiva ou negativa. E, também, os intervalos de crescimento e decrescimento da parábola:
- Ela é decrescente quando a derivada é negativa, ou seja, em ;
- Ela é crescente quando a derivada é positiva, ou seja, em .
Além disso, vemos que seu ponto de mínimo é o mesmo ponto do vértice.
Passo 7
Agora, vamos plotar o gráfico completo:
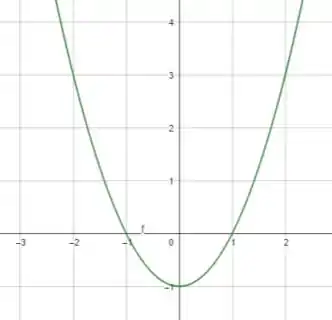
Entendeu direitinho? Responde aee ;)
Resposta
No texto