Cálculo 1 – 2ª Lista – 2023.1 – Exercício 1a
A demanda de um certo produto é unidades por mês quando o preço é p reais a unidade.
(a) Faça um gráfico dessa função de demanda.
Passo 1
Fala aí galera, bora resolver o nosso exercício? Vamos lá.
Bom, de acordo com o enunciado, a nossa função é:
Então, antes da gente pensar em esboçar o gráfico dela, temos que ver qual o grau da nossa função. Se a gente for reparar, a nossa variável não tem nenhum número no expoente dela, ou seja, podemos dizer que:
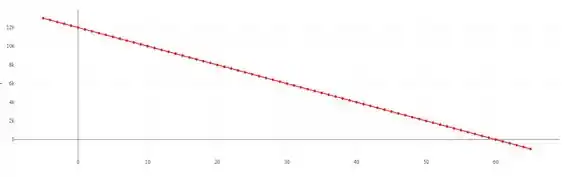
Ela está elevada a 1, então ela é uma função de primeiro grau. Logo, o gráfico da nossa função demanda será uma reta.
Para esboçarmos o gráfico de uma reta, vamos precisar de 2 pontos. Normalmente, os pontos escolhidos são os que a gente zera as nossas variáveis, então vamos usar:
Shoow, então, vamos lá.
Passo 2
Começando a calcular:
Substituindo:
Logo:
Passo 3
Calculando o segundo ponto
Substituindo:
Logo:
Passo 4
Beleza galera, já temos os nossos pontos, com isso, vamos poder traçar o nosso gráfico, ficando:
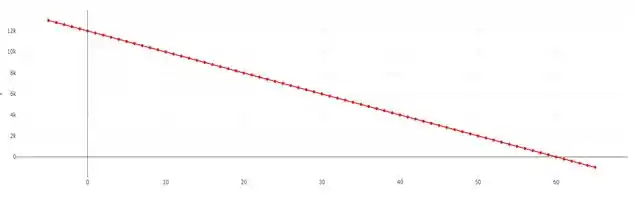
Resposta
