UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 20b
Determine e esboce o domínio da função:
b)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar o domínio (e seu esboço) da seguinte função:
O domínio de uma função trata-se do conjunto de todos os pares ordenados para os quais a função está definida.
Por exemplo, se a função estiver definida apenas para valores reais de e , então o domínio seria o conjunto de todos os pares ordenados pertencentes aos números reais.
Dessa forma, vemos que nossa função só existe se o radicando seja maior ou igual a zero, ou seja:
Lembrando que estamos trabalhando com números reais!!
Agora temos que resolver essa desigualdade!! Bora lá!
Passo 2
Bom... Resolvendo a inequação, temos:
Portanto, o domínio da função é o conjunto de todos os pares ordenados tais que , ou seja:
Ainda, em outras palavras, o domínio é o conjunto de todos os pontos acima ou sobre a parábola , ou seja, a região delimitada por essas duas parábolas.
Passo 3
Por fim, plotando o domínio da função, temos:
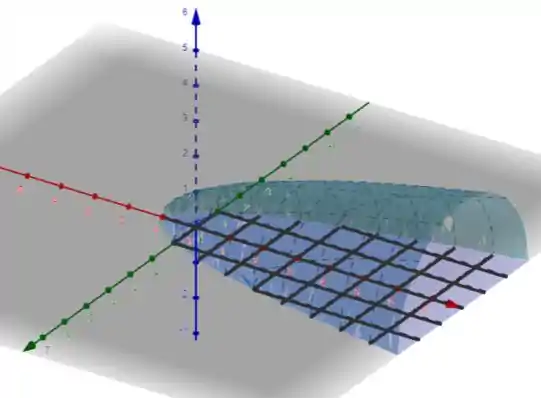
Onde a função é representada em azul claro e o domínio em roxo.
Entendeu direitinho? Responde aee ;)
