UTFPR, Sem Campus, Cálculo Diferencial e Integral 2, Listas de Cálculo 2 - Profº Ronie Peterson - Lista de Exercícios 1, Questão 4f
Determine e esboce o domínio das funções:
f)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para determinar e esboçar o domínio da seguinte função:
Lembrando que o domínio de uma função se trata do subconjunto de no qual todas as operações indicadas em são possíveis.
Passo 2
Bom... para que essa função exista, então:
Ou seja, temos que a função é válida para a seguinte interseção:
Passo 3
Dessa forma, plotando o domínio da função, temos:
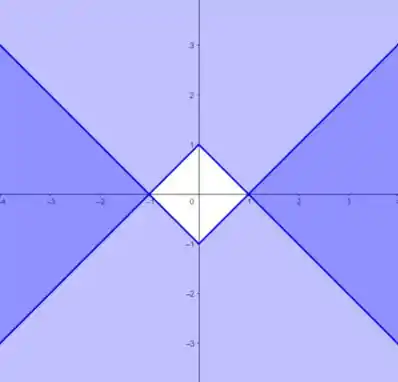
Entendeu direitinho? Responde aee ;)
Resposta
No texto
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica