UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.1a.
1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:
(a)
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nossa missão nesse problema é obter as raízes, os vértices e esboçar o gráfico da função .
Lembra como fazemos isso? 🤔
As raízes de uma função são dadas quando o gráfico da função cruza o eixo , ou seja, quando .
A partir de Bhaskara, as raízes são obtidas pelas fórmulas
Já os vértices podem ser obtidos através da formulinha
E a partir daí, podemos estimar o gráfico da função pelo que esperamos do seu comportamento.
Sacou, bora lá! 😁
Passo 2
Primeiro vamos obter as raízes de ...
Com as raízes obtidas, vamos obter o vértice...
Dessa forma, os pontos e são as raízes de e o ponto é o vértice de .
Tranquilo até aqui? 😉
Passo 3
Agora que encontramos esses pontos, vamos obter o gráfico de .
A função é uma parábola com a concavidade voltada para cima. Quando a função corta o eixo em
Plotando esses pontos e ligando esses pontos, podemos obter algo aproximadamente igual a
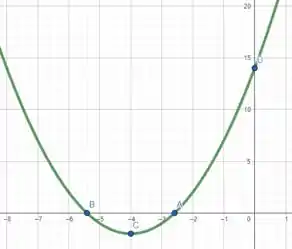
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
e são as raízes de e o ponto é o vértice de