UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.1b.
1. Determine os zeros (caso existam) e o vértice das funções quadráticas seguintes. Em seguida, esboce seus gráficos:
(b)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nossa missão nesse problema é obter as raízes, os vértices e esboçar o gráfico da função .
Lembra como fazemos isso? 🤔
As raízes de uma função são dadas quando o gráfico da função cruza o eixo , ou seja, quando .
A partir de Bhaskara, as raízes são obtidas pelas fórmulas
Já os vértices podem ser obtidos através da formulinha
E a partir daí, podemos estimar o gráfico da função pelo que esperamos do seu comportamento.
Sacou, bora lá! 😁
Passo 2
Primeiro vamos obter as raízes de ...
Caímos em uma raiz de número negativo, portanto, a função não tem raízes no conjunto dos números reais
Como as raízes não existem, vamos obter o vértice...
Dessa forma, não possui raízes, ou seja, o gráfico da função não corta o eixo , mas o vértice da função está no ponto .
Tranquilo até aqui? 😉
Passo 3
Agora que encontramos essas informações, vamos obter o gráfico de .
A função é uma parábola com a concavidade voltada para baixo. Quando a função corta o eixo em
Plotando esses pontos e ligando esses pontos, podemos obter algo aproximadamente igual a
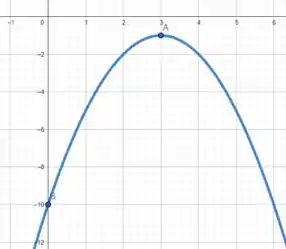
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
não possui raízes reais, mas o vértice da função está no ponto .