UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 9.1b.
1. Durante uma epidemia de dengue, o número de pessoas que adoeceram, num certo bairro, após dias é dado por:
(b) Esboce o gráfico de
Passo 1
Fala aí!! Bem-vindo! Está tendo um pouco de dificuldades nessa questão? Não se preocupe vou fazer o máximo pra te ajudar. 😉👍
Nesse problema queremos obter um esboço de gráfico da função .
Simples, não é? 😉
Para esboçar o gráfico da função , podemos seguir os seguintes passos:
Determinar o comportamento assintótico da função: Quando tende ao infinito, o termo exponencial tende a zero, o que significa que o denominador da função tende a 1. Portanto, quando tende ao infinito, tende a . Isso indica que o gráfico da função tem uma assíntota horizontal em .
Encontrar os interceptos com os eixos coordenados: Para encontrar o intercepto com o eixo , podemos definir e calcular :
Portanto, o intercepto com o eixo é .
Sacou? 👀
Passo 2
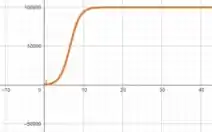
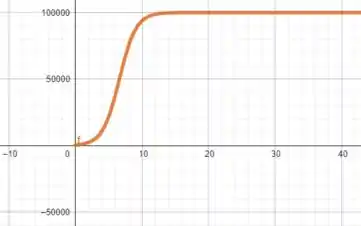
Assim como vimos no item anterior, quando tende a , a função se estabiliza em .
Se analisarmos a função , vemos que tende a muito rápido já que tende a muito rápido. Então podemos esperar que comece em como vimos no passo 1, tenha uma subida muito expressiva e se estabilize em .
Ou seja, mais ou menos assim...
É isso! Essa resolução te ajudou? Responde Aí! ✌
Resposta
