UFU, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profª Sonia Berrios - Lista 1 - Números Reais e Funções, Questão 12c
Encontre o domínio e faça um esboço do gráfico de cada função.
c)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos pede para esboçar a função e encontrar seu domínio!
Bom... o domínio trata-se dos números que a função não pode assumir para que a sua condição de existência não seja afetada.
Assim, temos que analisar a função e verificar quais são essas condições.
Não entendeu? Então bora junto 😉
Passo 2
Bom... primeiramente, com uma calculadora gráfica, podemos plotar a função :
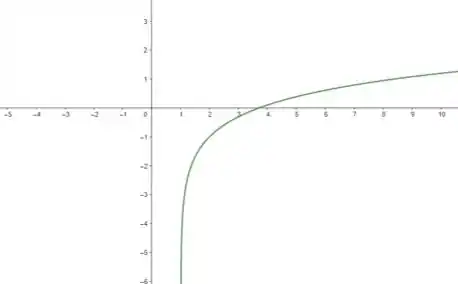
Passo 3
Analisando a função, vemos que para a função existir, então temos que o valor dentro de deve ser positivo, ou seja:
Dessa forma, dizemos que o seu domínio são todos os números reais maiores que , ou seja:
Entendeu direitinho? Responde aee ;)
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica