UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.7a.
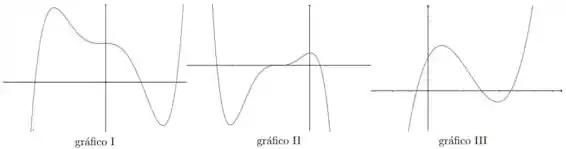
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico
(a) ;
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, queremos obter as raízes de e determinar qual dos gráficos melhor representa a função.
Como podemos fazer isso? 😎
Como a função é de grau muito alto, podemos usar o teorema das raízes racionais.
Nesse teorema, olhamos para o termo independente do polinômio, no caso: e para o termo associado à variável de maior grau, no caso: .
Esse teorema nos diz que as raízes de devem ser múltiplos da razão desses termos.
Além desses pontos, podemos obter o ponto em que cruza o eixo , ou seja, quando .
A partir desses pontos, podemos determinar qual dos gráficos é o da nossa função.
Bora lá! 😁
Passo 2
Primeiro definimos os múltiplos do termo independente
Agora para a constante associada ao termo de maior grau
Assim, os candidatos a raízes são as combinações de
Simplificando e eliminando os termos repetidos...
Assim os candidatos a raízes são , , , , e .
Substituindo em vemos quais fazem
Para :
Como , não é raiz.
Para :
Agora , logo é uma raiz
Para :
Da mesma forma, é raiz de !
Para :
Para :
Por fim, para :
Portanto, vemos que as raízes de são , e
Bacana, não é? 😉
Passo 3
Por último, vamos obter o valor em para vermos em qual ponto corta o eixo
Logo, é o ponto que corta o eixo .
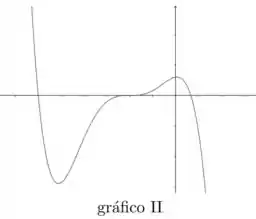
Analisando as opções, vemos que apenas um dos gráficos tem duas raízes negativas e uma raiz positiva.
Então o gráfico que melhor representa a função é o gráfico
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
As raízes de são , e ; gráfico