UFU, Sem Campus, Cálculo 1, Profº Sato - Listas de Cálculo 1 - 1ª Lista de Exercícios, Questão 2.7b.
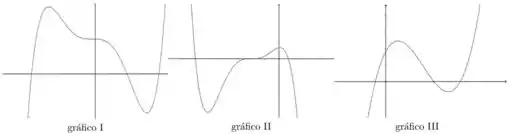
7. Encontre os zeros e estude o sinal das seguintes funções polinomiais. Em seguida associe cada função com seu gráfico
(b) ;
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, queremos obter as raízes de e determinar qual dos gráficos melhor representa a função.
Como podemos fazer isso? 😎
Nesse caso, a função não tem grau muito alto, então podemos obter as raízes de fatorando o polinômio e igualando a .
Depois disso, podemos obter o ponto em que corta o eixo , ou seja, quando
Com esses pontos obtidos, podemos estimar qual gráfico possui os mesmos pontos como raiz e .
Bora lá! 👀
Passo 2
Fatorando a função , temos
Igualando a , vamos obter que
Para a igualdade ser verdadeira, deve ser igual a e/ou deve ser igual a , ou seja
A primeira raiz que obtemos é
Obtendo as raízes de , temos
Aplicando o teorema de Bhaskara...
Logo, as raízes de são , e
Tranquilo até aqui? 😁
Passo 3
Agora, vamos obter o ponto que corta o eixo .
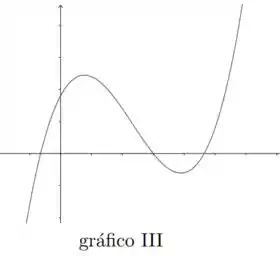
Assim, vemos que o gráfico que melhor representa nossa função é dado pelo gráfico , já que é próximo de e é próximo de e é outra raiz.
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
As raízes de são , e ; gráfico