Esboçar o gráfico de para diferentes valores de , incluindo os valores e
I)
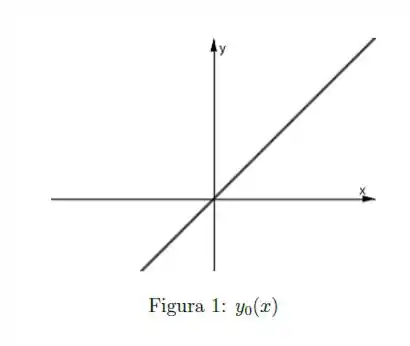
Passo 1
Oi, tudo bem? O problema pediu para esboçarmos o gráfico dessa função aqui
Para diferentes ! Então com ajuda do Geogebra vamos plotar esses gráficos?
Começando para , assim temos
É a abcissa dos quadrantes ímpares! É nossa conhecida!
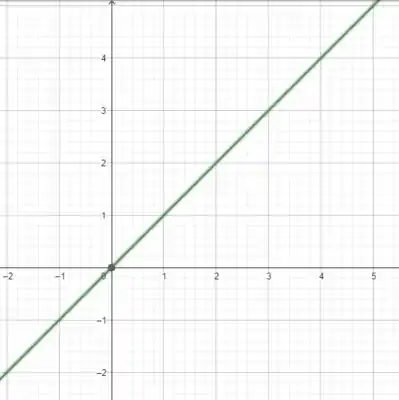
Beleza?
Passo 2
Vamos agora plotar com
Aqui temos uma soma de funções! Mais perto da origem, quem ‘ganha’ é o linear, já que a exponencial fica muito pequenininha. Já para valores maiores de a exponencial acaba ganhando!
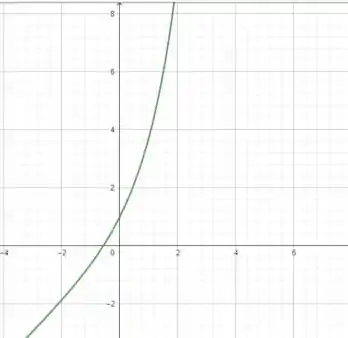
Passo 3
Agora vamos plotar para
A ideia aqui é a mesma! Perto da origem quem ganha é a parte linear, mas ao se afastar quem se sobressai é o
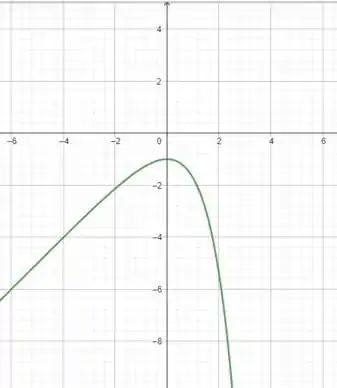
Show! E é isso pessoal! Espero ter ajudado!