UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 21a
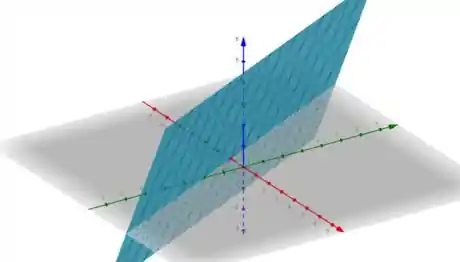
Esboce o gráfico de cada função a seguir:
a)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos esboçar o gráfico da seguinte função:
Para isso, temos que saber que a função define um plano em três dimensões, onde cada ponto no plano é associado a um valor em dado por .
Dessa forma, podemos esboçar o gráfico dessa função plotando os pontos que satisfazem a equação em um sistema de coordenadas cartesianas com três eixos e.
Mas vamos com calma juntinhos!! 😉
Passo 2
Para isso, podemos começar traçando o plano como um plano horizontal.
Em seguida, podemos traçar linhas com inclinação que partem de cada ponto no plano e se estendem para cima.
Lembra que cada ponto no plano é associado a um valor em dado por ?
Então a inclinação dessas linhas é determinada pela relação entre a variação em e a variação em e .
Essas linhas se encontram em um ponto no espaço que representa o valor máximo da função.
Passo 3
Dessa forma, o gráfico resultante é um plano inclinado em relação ao plano , com inclinação na direção do eixo .
Esse plano intersecta o eixo em , ou seja, a função assume o valor em .
Assim, plotando o gráfico, encontramos:
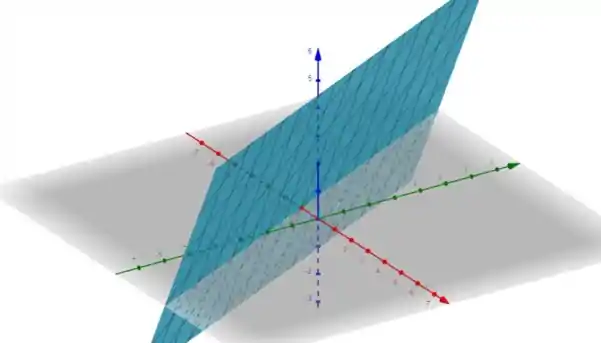
Onde a função está representada em azul.
Entendeu direitinho? Responde aee ;)
Resposta
