UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille - Segunda Lista de Exercícios, Questão 21d
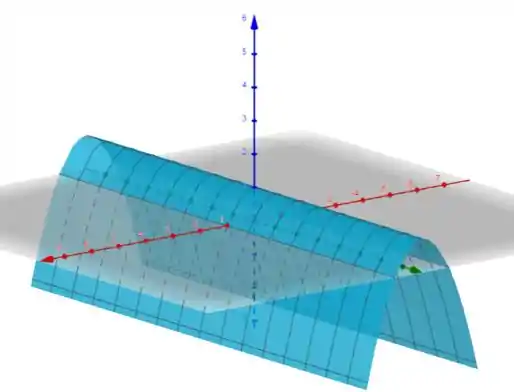
Esboce o gráfico de cada função a seguir:
d)
Passo 1
Eaee!!! Belezinha? Bom... a questão nos esboçar o gráfico da seguinte função:
Para isso, temos que saber que a função define um plano em três dimensões, onde cada ponto no plano é associado a um valor em dado por .
Dessa forma, podemos esboçar o gráfico dessa função plotando os pontos que satisfazem a equação em um sistema de coordenadas cartesianas com três eixos e.
Mas vamos com calma juntinhos!! 😉
Passo 2
Para isso, podemos começar traçando o plano como um plano horizontal.
Em seguida, podemos traçar curvas de nível para diferentes valores de , o que nos dará uma ideia da forma da superfície.
Para isso, podemos escolher alguns valores de e resolver a equação para obter as curvas correspondentes.
Por exemplo, quando , temos , o que nos dá uma curva de nível formada pelos pontos e no plano .
Podemos fazer o mesmo para outros valores de , como (que nos dá ) ou (que nos dá ).
Passo 3
Assim, plotando o gráfico, encontramos:
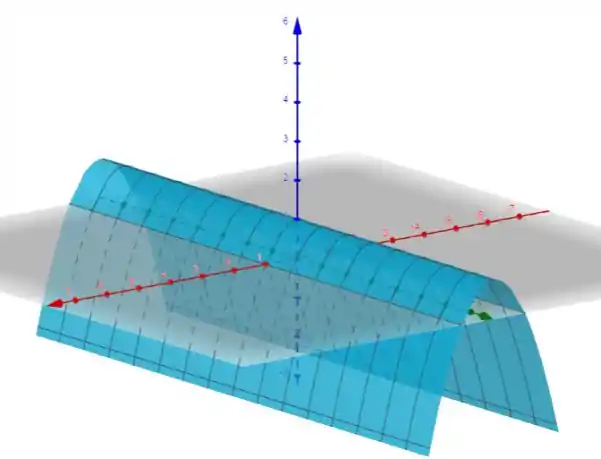
Onde a função está representada em azul.
Entendeu direitinho? Responde aee ;)
Resposta
