UFU – Cálculo 1 – Lista 1 – Questão 5d
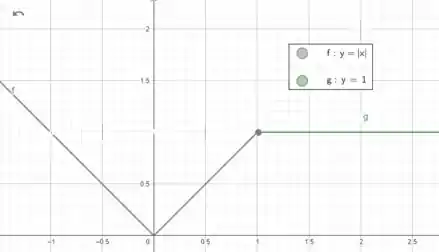
Esboce o gráfico da função
Passo 1
Oi pessoal, tudo bem? Vamos começar?
O problema começa nos dando essa função aqui:
E pediu para esboçar! Então vamos lá! Precisamos notar que essa é uma função definida por partes. Antes de temos o módulo de . Depois de temos uma reta horizontal com !
Tudo bem até aqui?
No nosso caso temos uma função contínua, pois em tanto a parte de cima quanto a de baixo valem .
Agora nossa missão é colocar as duas equações no mesmo plano!
Mas relaxa, vou fazer passo a passo com você!
Passo 2
Precisamos esboçar essas duas equações. Primeiro :
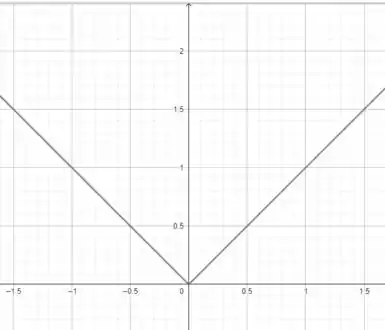
Beleza?
Depois :
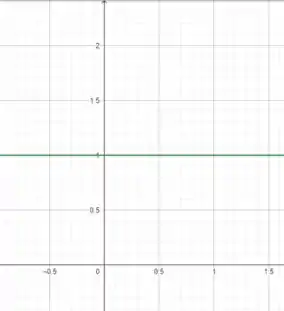
Tudo bem até aqui?
Agora vamos esboçar essas duas equações em um plano só! O módulo até e a reta horizontal em seguida!
Passo 3
Esboçando nossa função em um mesmo gráfico temos
E o esboço fica assim
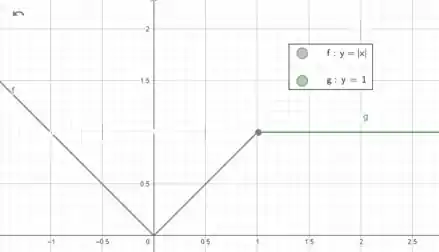
Beleza? Espero ter ajudado!
Até a próxima!
Resposta
