UFU – Cálculo 1 – Listas – Professor Sato
7.7 Esboce o gráfico das seguintes funções:
a)
b)
c)
d)
Passo 1
Falaaa.. beleza??
Nessa questão vamos esboçar o gráfico da função .
Pra isso vamos calcular o limite da função com tendendo a infinito e menos infinito. Daí achamos assíntotas horizontais.
Também vamos analisar os casos onde pode ter assíntota verticas, que é quando tem divisão por zero.
Passo 2
Fazendo:
Então temos a assíntota horizontal .
Passo 3
Repara que vamos ter divisão por zero, quando :
Então é assíntota vertical.
Ou quando :
Então é assíntota vertical.
Esboçando o gráfico:
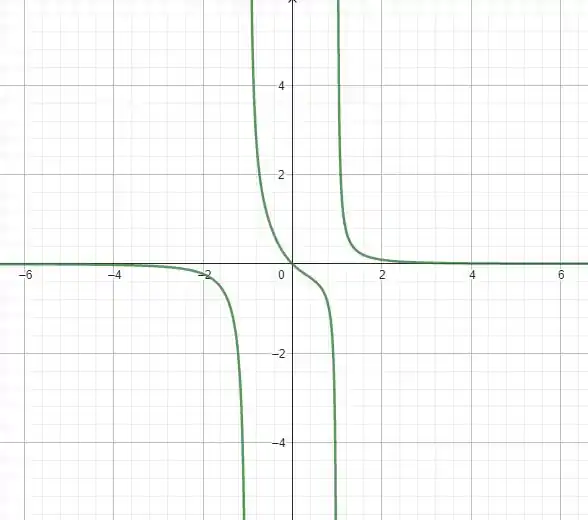
Resposta
Gráfico no último passo
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica