UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº José de Albuquerque - Lista de Gráficos, L'hopital e problemas de otimização, Questão 7b
7. Esboce o gráfico das seguintes funções:
b)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, queremos obter um esboço do gráfico da função .
Parece de boa, não é? 😁
Pra essa tarefa, podemos usar algumas artimanhas para nos ajudar, por exemplo encontrar os pontos da curva que cortam o eixo e o eixo .
Podemos também encontrar a derivada da função e descobrir em quais intervalos ela é crescente e em quais intervalos ela é crescente.
Vamos ver o que podemos fazer nesse caso! 👀
Passo 2
Primeiro vamos encontrar onde a função corta o eixo fazendo
Como essa função é de grau , nem sempre é simples obter as raízes, então vamos deixar esses dados pra lá.
Obtendo a derivada de para sabermos como é o seu comportamento, temos
Colocando em evidência...
Fazendo
Vemos que em e em a função possui tangencia , ou seja, a tangente da função nesses pontos é paralela ao eixo .
Analisando os sinais de
Temos que se , é menor que e, portanto, é decrescente, assim como se .
Mas se a função é crescente já que nesse intervalo.
Condensando essas informações em um gráfico, temos
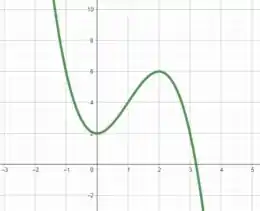
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
