UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº José de Albuquerque - Lista de Gráficos, L'hopital e problemas de otimização, Questão 7d
7. Esboce o gráfico das seguintes funções:
d)
Passo 1
Iae, como vai? Essa questão está um pouco complicada? Fique tranquilo que vamos tentar te ajudar. 😎👍
Nesse problema, queremos obter um esboço do gráfico da função .
Parece de boa, não é? 😁
Pra essa tarefa, podemos usar algumas artimanhas para nos ajudar, por exemplo encontrar os pontos da curva que cortam o eixo e o eixo .
Podemos também encontrar a derivada da função e descobrir em quais intervalos ela é crescente e em quais intervalos ela é crescente.
Vamos ver o que podemos fazer nesse caso! 👀
Passo 2
Primeiro vamos encontrar onde a função corta o eixo fazendo
Agora igualando a , podemos obter onde a função corta o eixo
Assim, vemos que a função passa pela origem do sistema.
Perceba que em a função possui uma descontinuidade, então vamos ver como ela se comporta nesse ponto.
Se se aproxima de para valores um pouco maiores o denominador tende a porém sempre com sinal positivo, ou seja
Já se se aproxima de mas com valores um pouco menores o denominador tende a mas sempre com valores negativos, ou seja
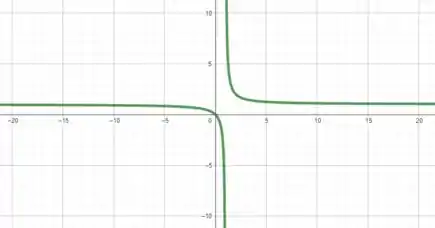
Assim, vemos que a função possui uma assíntota vertical em onde pela direita a função tende a e pela esquerda a função tende a .
Tranquilo até aqui? 😁
Passo 3
Agora vamos ver como a função se comporta em muito grande em modulo
Dividindo tudo por ...
Assim, quando aplicamos o limite, perceba que o termo tende a , então
Portanto, temos outra assíntota, dessa vez horizontal em .
Condensando essas informações em um gráfico, temos
E todos viveram felizes para sempre. Fim! 😉 Entendeu tudo? Responde Aí
Resposta
