UFPE, Sem Campus, Cálculo 1, Listas de Cálculo 1 - Profº José de Albuquerque - Lista de Gráficos, L'hopital e problemas de otimização, Questão 7f
7. Esboce o gráfico das seguintes funções:
f)
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema, queremos obter um esboço do gráfico da função .
Parece de boa, não é? 😁
Pra essa tarefa, podemos usar algumas artimanhas para nos ajudar, por exemplo encontrar os pontos da curva que cortam o eixo e o eixo .
Podemos também encontrar a derivada da função e descobrir em quais intervalos ela é crescente e em quais intervalos ela é crescente.
Vamos ver o que podemos fazer nesse caso! 👀
Passo 2
A primeira coisa que podemos perceber dessa função é que para menores que o termo não existe em .
Portanto, o gráfico de só vai existir para .
Fazendo para descobrir onde a função corta o eixo , temos
Agora fazendo para descobrir onde a função corta o eixo , temos
Então a função corta os eixos coordenados na origem do sistema e em .
Calculando a derivada de para descobrir seu comportamento, temos
Igualando a , temos
Assim, se a função possui uma tangente paralela ao eixo no ponto
Além disso, perceba que conforme aumenta, tende a pois o termo diminui cada vez mais.
Isso significa que para muito grande, a função se comporta como uma reta decrescente como , que possui uma tangencia de .
Obtendo alguns pontos de , temos
Então o ponto pertence a .
Condensando essas informações em um gráfico, temos
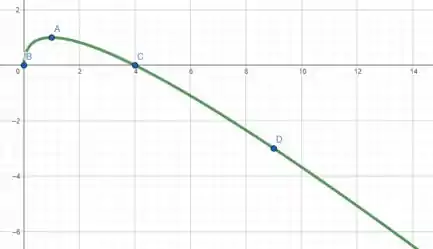
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
