USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4a
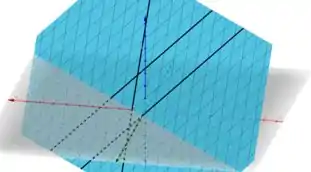
1.4. Esboce os gráficos de:
a.
Passo 1
Fala aí! Tudo certinho? Esta questão está um pouco complicada? Relaxa que vamos tentar te ajudar. 😎
Nesse problema queremos esboçar o gráfico da função .
Parece simples, não é? 😐
Para esboçar o gráfico de uma função tridimensional, podemos o método das seções...
Esse método consiste em fixar uma das variáveis a uma constante e obter uma curva bidimensional, assim, esboçando essa curva no plano onde fixamos a variável, podemos obter algumas “estruturas” do gráfico de .
Sacou como vai ser? 😁
Passo 2
Podemos começar fixando , ou seja
Agora com
E para
Esboçando contido no plano , em e em
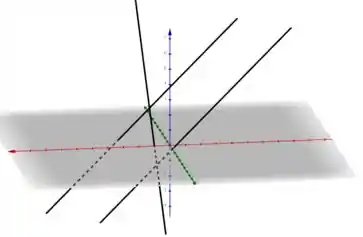
A partir daí e pelas características da função , podemos afirmar que é um plano
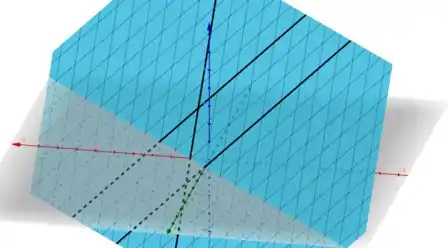
Fim! Iae, o que achou? Responde Aí! 😁
Resposta
Exercícios de Livros Relacionados
Esboce a curva polar. r = s e n4 θ
Elimine o parâmetro para encontrar uma equação cartesiana da curva:Esboce a curva e indique com uma seta a direção na qual a curva é traçada quando o parâmetro aumenta. x = senh t y = cosh t
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = d tem a equação polar r = e d 1 + e sen θ
Mostre que uma cônica com foco na origem, excentricidade e e diretriz y = - d tem a equação polar r = e d 1 - e sen θ
r = 9 6 + 2 cos θ (a) Encontre a excentricidade,(b) identifique a cônica,(c) dê uma equação da diretriz e(d) esboce a cônica