USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4b
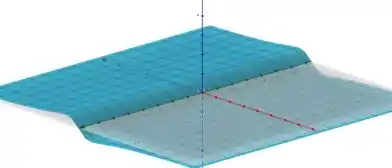
1.4. Esboce os gráficos de:
b.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema, nosso objetivo é obter o gráfico da função .
Tranquilo? 😉
Analisando a função, vemos que não varia, até porque nem está presente na função. Isso significa que se esboçarmos a função no plano , já vamos obter o gráfico em três dimensões.
Então podemos tratar a função inicialmente como bidimensional.
Bora começar! 😁
Passo 2
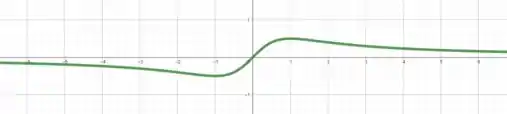
Vamos analisar algumas características da função...
Primeiro vemos que se trata da razão entre dois polinômios onde o polinômio do denominador é de maior grau. Assim se calcularmos limite de para vamos ver que a função tende a , ou seja, para grande, a função tende a nos dois lados do gráfico.
Além disso, podemos usar sua derivada para analisar o comportamento da função.
Pela regra do quociente, vamos obter
A partir dessa equação, vemos que se ou se a derivada é negativa, portanto, em e a função decresce.
Já entre , a derivada é positiva, logo a função é crescente!
Tranquilo até aqui? 👀
Passo 3
Vemos também que no denominador mesmo se for negativo, por estar elevado ao quadrado, sempre será positivo.
Já no numerador, o sinal de dita o sinal da função, então se , a função será negativa e se a função será positiva.
Quando , temos
Quando
Com as informações que obtemos até agora, podemos esboçar o gráfico da função bidimensional como
Sabendo que é constante em todo o domínio, o gráfico de será dado por
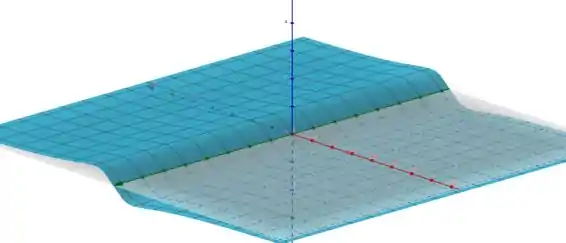
O que achou? Foi de boa? Responde aí! 😊
Resposta
