USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.4c
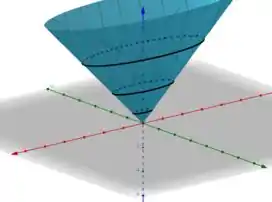
1.4. Esboce os gráficos de:
c.
Passo 1
E aí! Suave na nave?! Tá difícil essa questão? Relaxa que a gente vai te ajudar!
Nesse problema, estamos interessados em obter o gráfico da função .
Parece de boa? 🤔
Para esboçar o gráfico de uma função tridimensional, podemos o método das seções...
Esse método consiste em fixar uma das variáveis a uma constante e obter uma curva bidimensional, assim, esboçando essa curva no plano onde fixamos a variável, podemos obter algumas “estruturas” do gráfico de .
Sacou como vai ser? 😁
Passo 2
No nosso caso, temos algo interessante... perceba que na função temos uma raiz com e dentro, então podemos suspeitar que haja alguma simetria polar nesse problema.
Fazendo , então
Com isso, vemos que realmente há uma simetria polar na equação...
Nesse caso podemos definir que
Ou seja, para cada altura do plano , a função se comporta como uma elipse com e .
Por exemplo, para , temos
Para
E para
Bacana, não é? 😉
Passo 3
Plotando essas curvas cada uma em seu plano , vamos obter
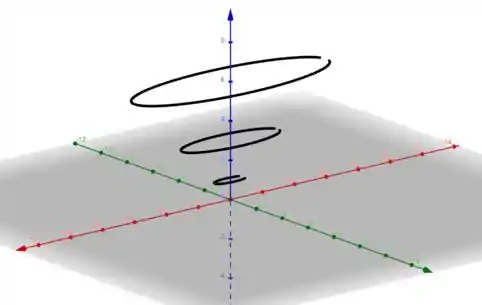
Assim, esboçando o gráfico de tendo em mente o padrão de repetição dos níveis obtidos...
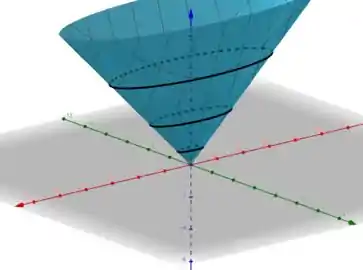
O que achou? Foi de boa? Responde aí! 😊
Resposta
